Swarm robotics

In a robotic swarm, many simple robots with limited individual capabilities perform a task in a decentralized and cooperative manner that otherwise would be impossible to achieve for a single robot. Each robot thereby acts only based on locally available information and communicates only with its nearest neighbors. The global behavior of the whole swarm emerges from the many local interactions of its members. The benefits of such an approach are given by the flexibility, scalability and robustness of the system.

Miniature swarm robot "Wanda"

When it comes to the design and analysis of the behavior of robotic swarms, the experimental evaluation is often very expensive. Therefore within the KIT project KITCoRoL, Marc Szymanski and Alexander Kettler developed the miniature swarm robot Wanda which now replaces the formerly used Jasmine robot. The goal of KITCoRoL is to provide an affordable, easy to manufacture but still very versatile and extensible platform for automated experiments with cooperating robots. The Wanda robot features a large number of different sensors, such as a color sensor, light sensors at the front-, bottom-, and top-side, an accelerometer or a battery monitor. Moreover it features a simple but efficient differential drive and a robust infrared communication and ranging system which is especially suited to be used in a large swarm of robots. There is a large number of Wanda robots available at the IPR institute together with an arena for swarm experiments.

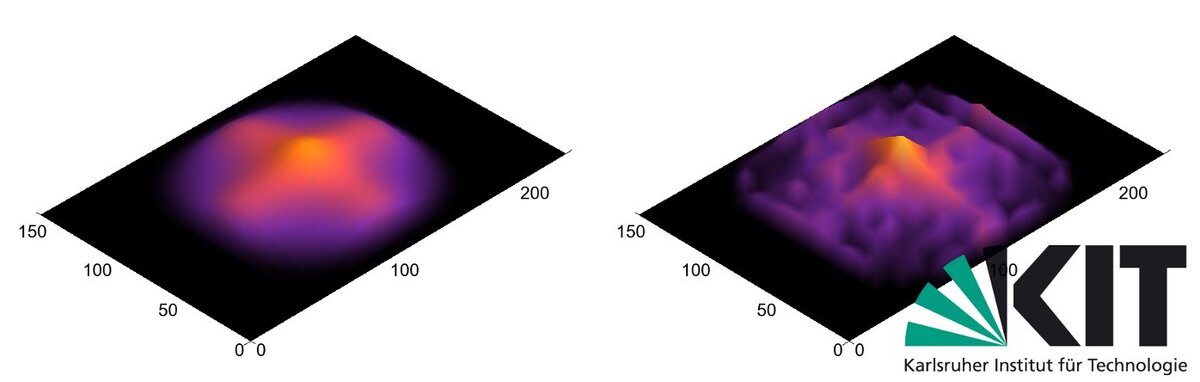
Simulation of robotic swarms

The most obvious method for the design and analysis of swarm algorithms is to run simulations. Due to the large number of robots the calculation of sensory data can become quite expensive especially if high accuracy is needed. Therefore at the IPR a new flexible simulation framework for robotic swarms is being developed which utilizes graphics hardware for these calculations. Experiments using the Wanda robot are being simulated using this framework.

Spatial models of robotic swarms

Besides experiments and simulations, mathematical models provide another possibility for the systematic analysis of the behaviour of robotic swarms.  Models derived in analogy to the Boltzmann-equation from statistical physics can be used to predict the temporal evolution of the spatial location probability of a robotic swarm without considering the single individuals of the swarm. The benefit of these methods is that their complexity remains constant independent of the size of the robotic swarm under investigation.